Introduzione alla funzione Dirac Delta

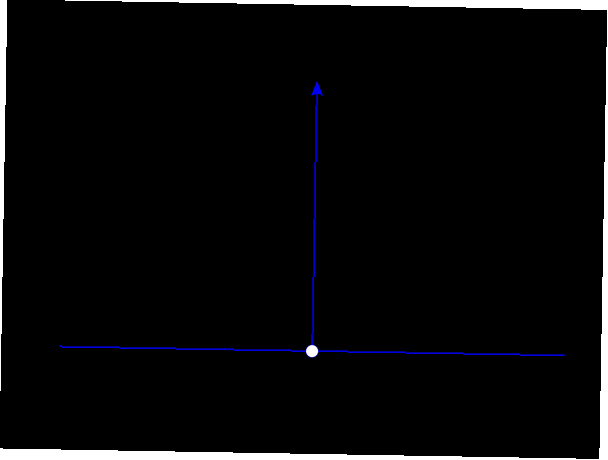
La funzione delta di Dirac è il nome dato a una struttura matematica che intende rappresentare un oggetto punto idealizzato, come una massa o carica di punti. Ha ampie applicazioni all'interno della meccanica quantistica e il resto della fisica quantistica, poiché viene solitamente utilizzato all'interno della funzione d'onda quantistica. La funzione delta è rappresentata con il delta del simbolo minuscolo greco, scritto come una funzione: δ (X).

Come funziona la funzione Delta

Questa rappresentazione si ottiene definendo la funzione delta di Dirac in modo che abbia un valore di 0 ovunque tranne che al valore di input di 0. A quel punto, rappresenta un picco che è infinitamente alto. L'integrale preso su tutta la linea è uguale a 1. Se hai studiato il calcolo, probabilmente ti sei imbattuto in questo fenomeno prima. Tieni presente che questo è un concetto che viene normalmente introdotto agli studenti dopo anni di studi universitari in fisica teorica.

In altre parole, i risultati sono i seguenti per la funzione delta più basilare δ (X), con una variabile monodimensionale X, per alcuni valori di input casuali:

• δ (5) = 0
• δ (-20) = 0
• δ (38.4) = 0
• δ (-12.2) = 0
• δ (0.11) = 0
• δ (0) = ∞

È possibile ridimensionare la funzione moltiplicandola per una costante. Secondo le regole del calcolo, la moltiplicazione per un valore costante aumenterà anche il valore dell'integrale per quel fattore costante. Poiché l'integrale di δ (X) tra tutti i numeri reali è 1, quindi moltiplicandolo per una costante di si avrebbe un nuovo integrale uguale a quella costante. Quindi, ad esempio, 27δ (X) ha un integrale tra tutti i numeri reali di 27.

Un'altra cosa utile da considerare è che poiché la funzione ha un valore diverso da zero solo per un input di 0, quindi se stai osservando una griglia di coordinate in cui il punto non è allineato a zero, questo può essere rappresentato con un'espressione all'interno dell'input di funzione. Quindi, se vuoi rappresentare l'idea che la particella sia in una posizione X = 5, quindi scrivere la funzione delta di Dirac come δ (x - 5) = ∞ [poiché δ (5 - 5) = ∞]. 

Se quindi si desidera utilizzare questa funzione per rappresentare una serie di particelle puntiformi all'interno di un sistema quantistico, è possibile farlo sommando varie funzioni dirac delta. Per un esempio concreto, una funzione con punti in x = 5 e x = 8 potrebbe essere rappresentata come δ (x - 5) + δ (x - 8). Se poi prendessi un integrale di questa funzione su tutti i numeri, otterrai un integrale che rappresenta numeri reali, anche se le funzioni sono 0 in tutte le posizioni diverse dalle due dove ci sono punti. Questo concetto può quindi essere espanso per rappresentare uno spazio con due o tre dimensioni (anziché il caso unidimensionale che ho usato nei miei esempi).

Questa è una breve introduzione ad un argomento molto complesso. La cosa fondamentale da capire a riguardo è che la funzione delta di Dirac esiste essenzialmente al solo scopo di dare un senso all'integrazione della funzione. Quando non si verifica alcun integrale, la presenza della funzione delta di Dirac non è particolarmente utile. Ma in fisica, quando hai a che fare con il passaggio da una regione senza particelle che improvvisamente esistono solo in un punto, è abbastanza utile.

Fonte della funzione Delta

Nel suo libro del 1930, Principi di meccanica quantistica, Il fisico teorico inglese Paul Dirac ha esposto gli elementi chiave della meccanica quantistica, tra cui la notazione bra-ket e anche la sua funzione delta di Dirac. Questi diventarono concetti standard nel campo della meccanica quantistica all'interno dell'equazione di Schrodinger.