Distribuzione normale standard in problemi di matematica

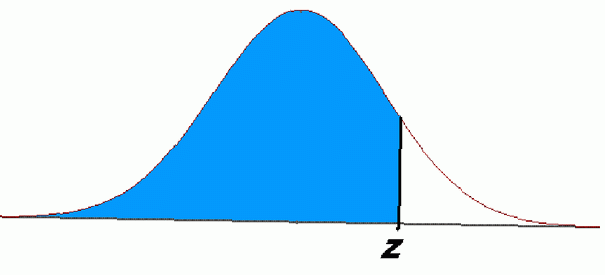
La distribuzione normale standard, che è più comunemente nota come curva a campana, si presenta in una varietà di luoghi. Diverse diverse fonti di dati sono normalmente distribuite. Di conseguenza, le nostre conoscenze sulla distribuzione normale standard possono essere utilizzate in diverse applicazioni. Ma non abbiamo bisogno di lavorare con una distribuzione normale diversa per ogni applicazione. Lavoriamo invece con una distribuzione normale con una media di 0 e una deviazione standard di 1. Vedremo alcune applicazioni di questa distribuzione che sono tutte legate a un particolare problema.

Esempio

Supponiamo che ci venga detto che le altezze dei maschi adulti in una particolare regione del mondo sono normalmente distribuite con una media di 70 pollici e una deviazione standard di 2 pollici.

1. Circa quale percentuale di maschi adulti è più alta di 73 pollici?
2. Quale percentuale di maschi adulti è compresa tra 72 e 73 pollici?
3. Quale altezza corrisponde al punto in cui il 20% di tutti i maschi adulti è maggiore di questa altezza?
4. Quale altezza corrisponde al punto in cui il 20% di tutti i maschi adulti è inferiore a questa altezza?

soluzioni

Prima di continuare, assicurati di fermarti e riprendere il lavoro. Di seguito una spiegazione dettagliata di ciascuno di questi problemi:

1. Usiamo il nostro z-formula del punteggio per convertire 73 in un punteggio standardizzato. Qui calcoliamo (73 - 70) / 2 = 1.5. Quindi la domanda diventa: qual è l'area sotto la distribuzione normale standard per z maggiore di 1,5? Consultare la nostra tabella di z-i punteggi ci mostrano che 0,933 = 93,3% della distribuzione dei dati è inferiore a z = 1,5. Pertanto il 100% - 93,3% = 6,7% dei maschi adulti è più alto di 73 pollici.
2. Qui convertiamo le nostre altezze in standard z-Punto. Abbiamo visto che 73 ha a z punteggio di 1,5. Il z-il punteggio di 72 è (72 - 70) / 2 = 1. Quindi stiamo cercando l'area sotto la distribuzione normale per 1<z < 1.5. A quick check of the normal distribution table shows that this proportion is 0.933 - 0.841 = 0.092 = 9.2%
3. Qui la domanda è capovolta da ciò che abbiamo già considerato. Ora guardiamo nella nostra tabella per trovare a z-Punto Z^* che corrisponde a un'area di 0,200 sopra. Per l'uso nella nostra tabella, notiamo che è qui che 0.800 è inferiore. Quando guardiamo il tavolo, lo vediamo z^* = 0,84. Dobbiamo ora convertire questo z-punteggio ad un'altezza. Da 0,84 = (x - 70) / 2, ciò significa che X = 71,68 pollici.
4. Possiamo usare la simmetria della distribuzione normale e risparmiarci il problema di cercare il valore z^*. Invece di z^* = 0,84, abbiamo -0,84 = (x - 70) / 2. così X = 68,32 pollici.

L'area della regione ombreggiata a sinistra di z nel diagramma sopra mostra questi problemi. Queste equazioni rappresentano probabilità e hanno numerose applicazioni in statistica e probabilità.