Il significato di mutua esclusività nelle statistiche

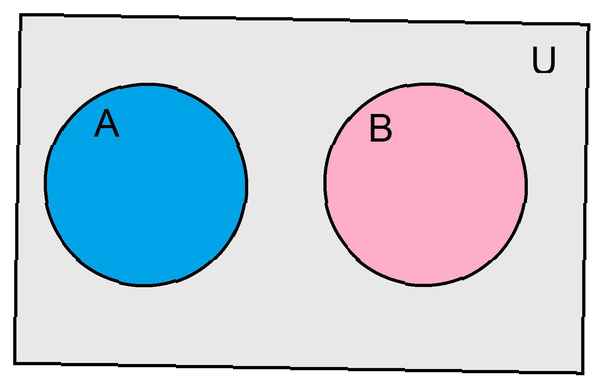
È probabile che due eventi si escludano a vicenda se e solo se gli eventi non hanno esiti condivisi. Se consideriamo gli eventi come insiemi, diremmo che due eventi si escludono a vicenda quando la loro intersezione è l'insieme vuoto. Potremmo denotare quegli eventi UN e B si escludono a vicenda dalla formula UN ∩ B = Ø. Come con molti concetti di probabilità, alcuni esempi aiuteranno a dare un senso a questa definizione.

Dadi rotolanti

Supponiamo di tirare due dadi a sei facce e aggiungere il numero di punti mostrati sopra i dadi. L'evento costituito da "la somma è pari" si esclude a vicenda dall'evento "la somma è dispari". La ragione di ciò è perché non è possibile che un numero sia pari e dispari.

Ora eseguiremo lo stesso esperimento di probabilità sul lancio di due dadi e sull'aggiunta dei numeri mostrati insieme. Questa volta considereremo l'evento consistente nell'avere una somma dispari e l'evento consisterà nell'avere una somma maggiore di nove. Questi due eventi non si escludono a vicenda.

Il motivo per cui è evidente quando esaminiamo i risultati degli eventi. Il primo evento ha esiti di 3, 5, 7, 9 e 11. Il secondo evento ha esiti di 10, 11 e 12. Poiché l'11 è in entrambi, gli eventi non si escludono a vicenda.

Carte da disegno

Illustriamo ulteriormente con un altro esempio. Supponiamo di pescare una carta da un mazzo standard di 52 carte. Disegnare un cuore non si esclude a vicenda all'evento di disegnare un re. Questo perché c'è una carta (il re dei cuori) che compare in entrambi questi eventi.

Perchè importa

Ci sono momenti in cui è molto importante determinare se due eventi si escludono a vicenda o meno. Sapere se due eventi si escludono a vicenda influenza il calcolo della probabilità che si verifichino l'uno o l'altro.

Torna all'esempio della carta. Se pesciamo una carta da un mazzo standard da 52 carte, qual è la probabilità che abbiamo pescato un cuore o un re?

Innanzitutto, suddividilo in singoli eventi. Per trovare la probabilità che abbiamo disegnato un cuore, prima contiamo il numero di cuori nel mazzo come 13 e poi dividiamo per il numero totale di carte. Ciò significa che la probabilità di un cuore è 13/52.

Per trovare la probabilità che abbiamo pescato un re, iniziamo contando il numero totale di re, risultando in quattro, e la successiva divisione per il numero totale di carte, che è 52. La probabilità che abbiamo disegnato un re è 4/52.

Il problema ora è trovare la probabilità di attirare un re o un cuore. Ecco dove dobbiamo stare attenti. È molto allettante aggiungere semplicemente le probabilità di 13/52 e 4/52 insieme. Ciò non sarebbe corretto perché i due eventi non si escludono a vicenda. Il re dei cuori è stato contato due volte in queste probabilità. Per contrastare il doppio conteggio, dobbiamo sottrarre la probabilità di disegnare un re e un cuore, che è 1/52. Pertanto la probabilità che abbiamo attirato un re o un cuore è 16/52.

Altri usi reciprocamente esclusivi

Una formula nota come regola di addizione offre un modo alternativo per risolvere un problema come quello sopra. La regola di addizione si riferisce in realtà a un paio di formule strettamente correlate tra loro. Dobbiamo sapere se i nostri eventi si escludono a vicenda per sapere quale formula di aggiunta è appropriata da utilizzare.