Le proprietà associative e commutative

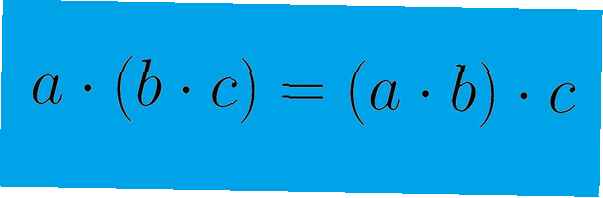
Esistono diverse proprietà matematiche utilizzate in statistica e probabilità; due di queste, le proprietà commutative e associative, sono generalmente associate all'aritmetica di base di numeri interi, razionali e numeri reali, sebbene compaiano anche in matematica più avanzata.

Queste proprietà, commutative e associative, sono molto simili e possono essere facilmente confuse. Per tale motivo, è importante comprendere la differenza tra i due.

La proprietà commutativa riguarda l'ordine di alcune operazioni matematiche. Per un'operazione binaria - una che coinvolge solo due elementi - questo può essere mostrato dall'equazione a + b = b + a. L'operazione è commutativa perché l'ordine degli elementi non influisce sul risultato dell'operazione. La proprietà associativa, d'altra parte, riguarda il raggruppamento di elementi in un'operazione. Questo può essere mostrato dall'equazione (a + b) + c = a + (b + c). Il raggruppamento degli elementi, come indicato dalle parentesi, non influisce sul risultato dell'equazione. Si noti che quando viene utilizzata la proprietà commutativa, gli elementi in un'equazione sono riarrangiato. Quando viene utilizzata la proprietà associativa, gli elementi sono semplicemente raggruppate.

Proprietà commutativa

In poche parole, la proprietà commutativa afferma che i fattori in un'equazione possono essere riorganizzati liberamente senza influire sul risultato dell'equazione. La proprietà commutativa, quindi, si occupa dell'ordinamento delle operazioni, inclusa l'aggiunta e la moltiplicazione di numeri reali, numeri interi e numeri razionali.

Ad esempio, i numeri 2, 3 e 5 possono essere sommati in qualsiasi ordine senza influire sul risultato finale:

2 + 3 + 5 = 10

3 + 2 + 5 = 10

5 + 3 + 2 = 10

Allo stesso modo i numeri possono essere moltiplicati in qualsiasi ordine senza influire sul risultato finale:

2 x 3 x 5 = 30

3 x 2 x 5 = 30

5 x 3 x 2 = 30

Sottrazione e divisione, tuttavia, non sono operazioni che possono essere commutative perché l'ordine delle operazioni è importante. I tre numeri sopra non può, ad esempio, essere sottratto in qualsiasi ordine senza influire sul valore finale:

2-3-5 = -6

3 - 5 - 2 = -4

5 - 2 - 2 = 0