Insiemistica

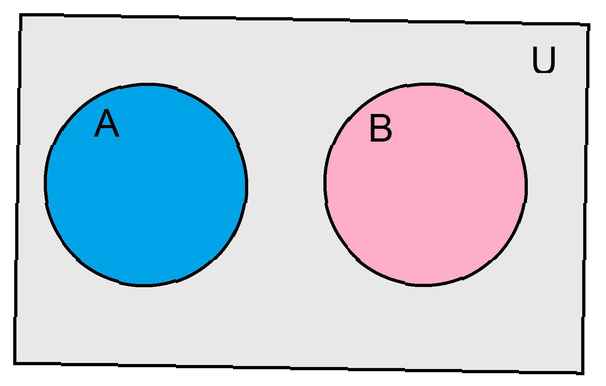
La teoria degli insiemi è un concetto fondamentale in tutta la matematica. Questo ramo della matematica costituisce una base per altri argomenti. 

Intuitivamente un insieme è una raccolta di oggetti, chiamati elementi. Anche se questa sembra un'idea semplice, ha alcune conseguenze di vasta portata. 

Elementi

Gli elementi di un set possono davvero essere qualsiasi cosa: numeri, stati, automobili, persone o anche altri set sono tutte possibilità per gli elementi. Quasi tutto ciò che può essere raccolto insieme può essere usato per formare un set, anche se ci sono alcune cose di cui dobbiamo stare attenti.

Set uguali

Gli elementi di un set sono in un set o no in un set. È possibile descrivere un set in base a una proprietà di definizione oppure elencare gli elementi nel set. L'ordine in cui sono elencati non è importante. Quindi gli insiemi 1, 2, 3 e 1, 3, 2 sono insiemi uguali, perché entrambi contengono gli stessi elementi.

Due set speciali

Due set meritano una menzione speciale. Il primo è l'insieme universale, tipicamente indicato U. Questo set comprende tutti gli elementi tra cui possiamo scegliere. Questo set può essere diverso da un'impostazione alla successiva. Ad esempio, un set universale può essere l'insieme di numeri reali mentre per un altro problema l'insieme universale può essere i numeri interi 0, 1, 2, .... 

L'altro set che richiede attenzione è chiamato set vuoto. Il set vuoto è il set univoco è il set senza elementi. Possiamo scrivere questo come e denotare questo set con il simbolo ∅.

Sottoinsiemi e Power Set

Una raccolta di alcuni degli elementi di un set UN viene chiamato un sottoinsieme di UN. Lo diciamo UN è un sottoinsieme di B se e solo se ogni elemento di UN è anche un elemento di B. Se è presente un numero finito n di elementi in un set, quindi ci sono un totale di 2ⁿ sottoinsiemi di UN. Questa raccolta di tutti i sottoinsiemi di UN è un set chiamato set di potenze di UN.

Impostare le operazioni

Proprio come possiamo eseguire operazioni come l'addizione - su due numeri per ottenere un nuovo numero, le operazioni di teoria degli insiemi vengono utilizzate per formare un insieme da altri due insiemi. Esistono numerose operazioni, ma quasi tutte sono composte dalle seguenti tre operazioni:

• Unione - Un'unione significa un incontro. L'unione dei set UN e B consiste degli elementi che si trovano in entrambi UN o B.
• Intersezione: un'intersezione è il punto in cui due cose si incontrano. L'intersezione degli insiemi UN e B consiste degli elementi che in entrambi UN e B.
• Complemento: il complemento dell'insieme UN è costituito da tutti gli elementi dell'insieme universale che non sono elementi di UN.

Diagrammi di Venn

Uno strumento utile per descrivere la relazione tra diversi insiemi è chiamato diagramma di Venn. Un rettangolo rappresenta l'insieme universale per il nostro problema. Ogni set è rappresentato con un cerchio. Se i cerchi si sovrappongono tra loro, questo illustra l'intersezione dei nostri due set. 

Applicazioni di Set Theory

La teoria degli insiemi è usata in tutta la matematica. È usato come base per molti sottocampi della matematica. Nelle aree relative alla statistica, è particolarmente usato nella probabilità. Gran parte dei concetti in probabilità derivano dalle conseguenze della teoria degli insiemi. In effetti, un modo per affermare gli assiomi della probabilità consiste nella teoria degli insiemi.