Foglio di lavoro per la disuguaglianza di Chebyshev
 Share
Share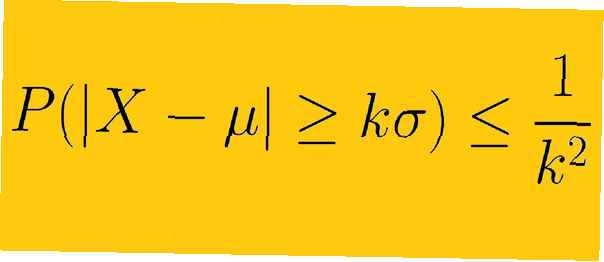
La disuguaglianza di Chebyshev afferma che almeno 1 -1 /K2 dei dati di un campione deve rientrare in K deviazioni standard dalla media, dove K è un numero reale positivo maggiore di uno. Ciò significa che non abbiamo bisogno di conoscere la forma della distribuzione dei nostri dati. Con solo la media e la deviazione standard, possiamo determinare la quantità di dati un certo numero di deviazioni standard dalla media.
Di seguito sono riportati alcuni problemi da esercitarsi utilizzando la disuguaglianza.
Esempio 1
Una classe di seconda elementare ha un'altezza media di cinque piedi con una deviazione standard di un pollice. Almeno quale percentuale della classe deve essere compresa tra 4'10 "e 5'2"?
Soluzione
Le altezze indicate nella gamma sopra sono entro due deviazioni standard dall'altezza media di cinque piedi. La disuguaglianza di Chebyshev dice che almeno 1 - 1/22 = 3/4 = 75% della classe rientra nell'intervallo di altezza indicato.
Esempio n. 2
Si ritiene che i computer di una determinata azienda durino in media tre anni senza alcun malfunzionamento dell'hardware, con una deviazione standard di due mesi. Almeno quale percentuale di computer dura tra 31 e 41 mesi?
Soluzione
La durata media di tre anni corrisponde a 36 mesi. I tempi da 31 mesi a 41 mesi sono ciascuno 5/2 = 2,5 deviazioni standard dalla media. Dalla disuguaglianza di Chebyshev, almeno 1 - 1 / (2.5) 62 = 84% dei computer dura da 31 mesi a 41 mesi.
Esempio n. 3
I batteri in una cultura vivono per un tempo medio di tre ore con una deviazione standard di 10 minuti. Almeno quale frazione di batteri vive tra due e quattro ore?
Soluzione
Due e quattro ore sono a un'ora di distanza dalla media. Un'ora corrisponde a sei deviazioni standard. Quindi almeno 1 - 1/62 = 35/36 = il 97% dei batteri vive tra due e quattro ore.
Esempio n. 4
Qual è il numero più piccolo di deviazioni standard dalla media che dobbiamo andare se vogliamo assicurarci di avere almeno il 50% dei dati di una distribuzione?
Soluzione
Qui usiamo la disuguaglianza di Chebyshev e lavoriamo all'indietro. Vogliamo il 50% = 0,50 = 1/2 = 1 - 1 /K2. L'obiettivo è usare l'algebra per risolvere K.
Vediamo che 1/2 = 1 /K2. Croce moltiplicare e vedere che 2 =K2. Prendiamo la radice quadrata di entrambi i lati e da allora K è un numero di deviazioni standard, ignoriamo la soluzione negativa all'equazione. Questo dimostra che K è uguale alla radice quadrata di due. Quindi almeno il 50% dei dati è all'interno di circa 1,4 deviazioni standard dalla media.
Esempio n. 5
La linea bus n. 25 impiega un tempo medio di 50 minuti con una deviazione standard di 2 minuti. Un poster promozionale per questo sistema di autobus afferma che "il 95% della linea 25 dell'autobus dura da ____ a _____ minuti". Con quali numeri riempire gli spazi vuoti?
