Cosa sono gli assiomi di probabilità?

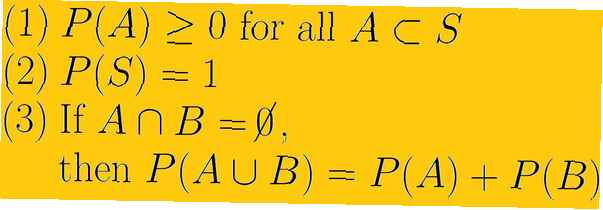
Una strategia in matematica è iniziare con alcune affermazioni, quindi costruire più matematica da queste affermazioni. Le dichiarazioni iniziali sono note come assiomi. Un assioma è in genere qualcosa che è matematicamente evidente. Da un elenco relativamente breve di assiomi, la logica deduttiva viene utilizzata per provare altre affermazioni, chiamate teoremi o proposizioni.

L'area della matematica conosciuta come probabilità non è diversa. La probabilità può essere ridotta a tre assiomi. Questo fu fatto per la prima volta dal matematico Andrei Kolmogorov. La manciata di assiomi che sono alla base della probabilità può essere utilizzata per dedurre tutti i tipi di risultati. Ma quali sono questi assiomi di probabilità?

Definizioni e preliminari

Per comprendere gli assiomi per probabilità, dobbiamo prima discutere alcune definizioni di base. Supponiamo di avere un insieme di risultati chiamato spazio campione S. Questo spazio campione può essere pensato come il set universale per la situazione che stiamo studiando. Lo spazio di esempio è composto da sottoinsiemi chiamati eventi E₁, E₂,... , E_n. 

Partiamo anche dal presupposto che esiste un modo per assegnare una probabilità a qualsiasi evento E. Questo può essere pensato come una funzione che ha un set per un input e un numero reale come output. La probabilità dell'evento E è indicato da P(E).

Axiom One

Il primo assioma della probabilità è che la probabilità di qualsiasi evento sia un numero reale non negativo. Ciò significa che il minimo che una probabilità possa mai essere è zero e che non può essere infinito. L'insieme di numeri che possiamo usare sono numeri reali. Ciò si riferisce sia ai numeri razionali, noti anche come frazioni, sia ai numeri irrazionali che non possono essere scritti come frazioni.

Una cosa da notare è che questo assioma non dice nulla su quanto grande possa essere la probabilità di un evento. L'assioma elimina la possibilità di probabilità negative. Riflette l'idea che la probabilità minima, riservata agli eventi impossibili, è zero.

Assioma Due

Il secondo assioma della probabilità è che la probabilità dell'intero spazio del campione sia una. Simbolicamente scriviamo P(S) = 1. In questo assioma è implicita l'idea che lo spazio del campione sia tutto possibile per il nostro esperimento di probabilità e che non vi siano eventi al di fuori dello spazio del campione.

Di per sé, questo assioma non stabilisce un limite superiore per le probabilità di eventi che non sono l'intero spazio del campione. Riflette che qualcosa con assoluta certezza ha una probabilità del 100%.

Assioma Tre

Il terzo assioma della probabilità si occupa di eventi reciprocamente esclusivi. Se E₁ e E₂ si escludono a vicenda, nel senso che hanno un'intersezione vuota e quindi usiamo U per indicare l'unione P(E₁ U E₂ ) = P(E₁) + P(E₂).

L'assioma in realtà copre la situazione con diversi eventi (anche numerabili infiniti), ognuno dei quali si escludono a vicenda. Finché ciò accade, la probabilità dell'unione degli eventi è la stessa della somma delle probabilità:

P(E₁ U E₂ U ... U E_n ) = P(E₁) + P(E₂) + ... + E_n

Anche se questo terzo assioma potrebbe non sembrare così utile, vedremo che combinato con gli altri due assiomi è piuttosto potente.

Applicazioni Axiom

I tre assiomi fissano un limite superiore per la probabilità di qualsiasi evento. Indichiamo il complemento dell'evento E di E^C. Dalla teoria degli insiemi, E e E^C hanno un incrocio vuoto e si escludono a vicenda. inoltre E U E^C = S, l'intero spazio del campione.

Questi fatti, combinati con gli assiomi ci danno: