La regola del complemento

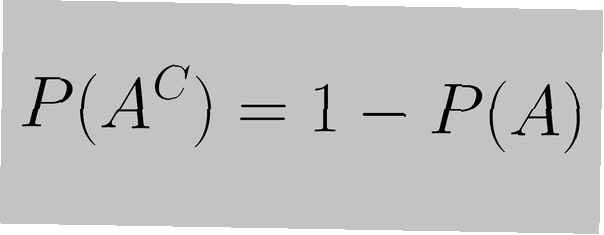
In statistica, la regola del complemento è un teorema che fornisce una connessione tra la probabilità di un evento e la probabilità del complemento dell'evento in modo tale che se conosciamo una di queste probabilità, allora conosciamo automaticamente l'altra.

La regola del complemento è utile quando calcoliamo determinate probabilità. Molte volte la probabilità di un evento è complicata o complicata da calcolare, mentre la probabilità del suo complemento è molto più semplice.

Prima di vedere come viene utilizzata la regola del complemento, definiremo in modo specifico quale sia questa regola. Iniziamo con un po 'di notazione. Il complemento dell'evento UN, costituito da tutti gli elementi nello spazio campione S che non sono elementi dell'insieme UN, è indicato da UNC.

Dichiarazione della regola del complemento

La regola del complemento è definita come "la somma della probabilità di un evento e la probabilità del suo complemento è uguale a 1", espressa dalla seguente equazione:

P (UN^C) = 1 - P (UN)

L'esempio seguente mostrerà come utilizzare la regola del complemento. Sarà evidente che questo teorema accelererà e semplificherà i calcoli delle probabilità.

Probabilità senza la regola del complemento

Supponiamo di lanciare otto monete giuste - qual è la probabilità che abbiamo almeno una testa che mostra? Un modo per capirlo è calcolare le seguenti probabilità. Il denominatore di ciascuno è spiegato dal fatto che ci sono 2⁸ = 256 risultati, ognuno ugualmente probabile. Tutti i seguenti ci formula per combinazioni:

• La probabilità di lanciare esattamente una testa è C (8,1) / 256 = 8/256.
• La probabilità di lanciare esattamente due teste è C (8,2) / 256 = 28/256.
• La probabilità di lanciare esattamente tre teste è C (8,3) / 256 = 56/256.
• La probabilità di lanciare esattamente quattro teste è C (8,4) / 256 = 70/256.
• La probabilità di lanciare esattamente cinque teste è C (8,5) / 256 = 56/256.
• La probabilità di lanciare esattamente sei teste è C (8,6) / 256 = 28/256.
• La probabilità di lanciare esattamente sette teste è C (8,7) / 256 = 8/256.
• La probabilità di lanciare esattamente otto teste è C (8,8) / 256 = 1/256.

Questi eventi si escludono a vicenda, quindi sommiamo le probabilità insieme usando una delle regole di addizione appropriate. Ciò significa che la probabilità che abbiamo almeno una testa è 255 su 256.

Utilizzo della regola del complemento per semplificare i problemi di probabilità

Ora calcoliamo la stessa probabilità utilizzando la regola del complemento. Il complemento dell'evento "Facciamo girare almeno una testa" è l'evento "Non ci sono teste". C'è un modo perché ciò avvenga, dandoci la probabilità di 1/256. Usiamo la regola del complemento e scopriamo che la nostra probabilità desiderata è una meno una su 256, che è uguale a 255 su 256.

Questo esempio dimostra non solo l'utilità ma anche il potere della regola del complemento. Sebbene non ci sia nulla di sbagliato nel nostro calcolo originale, è stato piuttosto coinvolto e ha richiesto più passaggi. Al contrario, quando abbiamo usato la regola del complemento per questo problema non c'erano molti passaggi in cui i calcoli potevano andare male.